

O Prolegômenos à Academia de Lógica é um curso de lógica do Professor Victorelli. Neste documento, traremos notas de aula. Este documento não é uma transcrição do curso e não dispensa que o aluno assista-o em sua completude. O intuito deste documento é servir como material de consulta, revisão e fixação dos conteúdos presentes nas aulas do curso, por isso é importante que o aluno já tenha concluído as aulas referentes às seções. O documento tem vinte e duas seções, coincidindo com o número de aulas. Por isso, é interessante assistir uma aula, fazer suas próprias anotações e depois ler a seção correspondente para encadear o que estudou. Lembre-se também que no módulo do curso, há um PDF com a lousa, que também será muito útil caso o aluno queira realizar uma revisão mais ilustrativa.
A nossa inteligência trabalha com abstrações, recortes da realidade. Torna particular aquilo que é geral, divide em partes simples aquilo que é composto, o processo de recortar algo da realidade, a fim de tornar possível o ato de raciocínio é chamado de abstração.
Apresentaremos os conceitos de percepto, fantasma1 e conceito usando uma analogia: imagine que você está diante de uma belíssima paisagem natural, o encontro dos sentidos externos (visão, audição, olfato, tato ou paladar) com a realidade (a imagem real da paisagem) é chamado de percepto. A visão imediata da bela paisagem chegando aos seus olhos é uma apreensão sensível da realidade, ela está ali, diante dos seus olhos. Agora imagine que você se virou de costas e ainda deseja visualizar essa paisagem, você já a viu anteriormente. Agora, a sua mente é capaz de evocar um fantasma da imagem previamente vista com seus próprios olhos, você é capaz de visualizar essa paisagem através de uma imagem mental da paisagem real, essa imagem não é perfeita, é claro, mas é uma representação da realidade. Essa imagem que é guardada na mente depois do encontro dos sentidos com a realidade é chamada de fantasma. O percepto tem relação com os cinco sentidos externos, o fantasma tem relação com os sentidos internos, pela própria natureza evocativa, donde o movimento do intelecto é em parte do interno (imaginação) para o externo (evocação da imagem externa), essa imagem não é uma representação exatamente fidedigna à realidade.
Agora, imagine uma outra situação: existe uma pequena menina, essa menina viu apenas um único cachorro durante toda a sua vida, mas, depois de um tempo, ela encontra um outro cachorro individual. Essa menina será capaz de identificar que esse indivíduo particular novo e inédito faz parte do mesmo conjunto do cachorro que ela já tinha visto previamente? A resposta é que sim, mas como que uma criança pequena pode ser capaz de identificar isso espontaneamente? A resposta é que essa criança abstraiu daquele primeiro cachorro algo que a ele é essencial: o seu conceito. Essa menina não se ateve à cor do cachorro, pois o novo cachorro é de uma cor diferente, ela também não se ateve ao tamanho ou aspectos acessórios. Essa menina só conseguiu identificar que esse novo indivíduo faz parte do conjunto de cachorros porque do primeiro cachorro, ela entendeu aquilo que àquele indivíduo é essencial, e, a partir daqui, podemos dizer que a criança passou pela apreensão sensível do indivíduo (percepto), retenção da imagem (fantasma) e, posteriormente, a formação do conceito (concepção). O percepto diz respeito aos sentidos externos, o fantasma, aos internos, e a concepção, ás faculdades intelectivas.
Em síntese:
Percepto: O encontro dos sentidos com a realidade, a apreensão sensível imediata.
Fantasma: A imagem mental criada pelos sentidos internos, fundamentalmente pela imaginação.
Conceito: A abstração criada pelas faculdades intelectivas daquilo que ao sujeito lhe é essencial.
A lógica é a ciência dos entes de razão de segunda intenção, temos entes reais e entes de razão. Entes reais são aqueles que existem fundamentalmente na realidade mesma, por exemplo uma cadeira individual, ou uma pessoa particular. Já os entes de razão, são aquelas coisas que são criadas pela mente: argumentos, proposições e termos são exemplos de entes de razão. Os entes reais têm a característica de serem sempre singulares. Uma cadeira real não é a mesma que outra cadeira, mesmo que elas sejam materialmente idênticas. Na realidade e nos entes reais, não existe identidade tomada na acepção absoluta, bem como é sensato dizer que os entes reais são cronotópicos (têm tempo e espaço). Já os entes de razão, por sua vez, são gerais e abstratos no sentido de serem recortes da realidade. Eles são gerais porque representam conceitos. Por exemplo: O conceito de mesa é aplicável a todas as mesas particulares, por isso, é correto entendermos os conceitos e a essência como fatores de unidade, não em acepção absoluta, mas em relativa. Os entes de razão podem ter identidade, os entes de razão são inspaciais e intemporais, contrariamente aos entes reais.
Os entes de razão podem ser usados em primeira intenção, isto é, referindo-se aos entes reais de alguma forma, bem como podem ser usados em segunda intenção, que é quando um ente de razão refere-se a si mesmo como um conceito. Os entes de razão de primeira intenção são abstraídos dos entes reais, já os entes de razão de segunda intenção são abstraídos dos entes de razão de primeira intenção. Termos são exemplos de entes de razão que possuem intenção, um termo é uma palavra usada para se referir a alguma coisa da realidade. Uma palavra é um mero veículo verbal, quando esse veículo verbal passa a representar algum conceito ou alguma coisa na realidade, dizemos que é um termo, podemos dizer também que um termo é a representação verbal de um conceito.
Em síntese:
Primeira Intenção: Um ente de razão usado com referência à realidade.
Exemplo: Esta esquadra é um quadrado. (Quadrado está em primeira intenção).
Segunda Intenção: Um ente de razão usado com referência a si mesmo como um conceito.
Exemplo: Quadrado é um conceito geométrico. (Quadrado está em segunda intenção).
A intensão de um termo é o conjunto de notas que contemplam toda a amplitude do conceito. A intensão do termo cadeira é ser um assento desenvolvido para acomodar uma única pessoa. A intensão do termo Deus é (em termos equívocos2) ser onipotente, onisciente, onibenevolente e onipresente. Podemos entender que a intensão de um termo é a soma das características essenciais que o termo implica, é seu significado por excelência.
Já a extensão de um termo, é o conjunto de indivíduos que a intensão contempla. Podemos pensar que a extensão do termo cadeira é todas as cadeiras particulares. Podemos também pensar que a extensão do termo homem é o conjunto de todos os homens do planeta.
Podemos, de certa e equívoca forma. entender intensão como sendo o aspecto qualitativo de um termo, e a extensão como sendo seu aspecto quantitativo.
Quanto mais um termo aumenta em intensão, mais ele diminui em extensão. Quanto mais ele aumenta em extensão, mais diminui em intensão.
Conceitos são representações intelectuais de objetos. É a abstração da realidade, um recorte que a mente faz através do intelecto, para que possamos entendê-la mais propriamente. Conceitos podem ser superiores ou inferiores. Um conceito é superior quando ele abrange extensionalmente o inferior, um conceito é inferior quando ele é abrangido extensionalmente pelo superior. O conceito de homem é abrangido extensionalmente pelo conceito superior (que é animal). Veja o Notas - Isagoge & Categorias para uma explicação mais detalhada dos predicáveis, tema muito próximo do que estamos tratando aqui. Resumidamente, tomando como exemplo o termo homem, fica claro dizer que homem é uma espécie de animal, e que, por sua vez, animal é um gênero de homem. Disso, dizemos que animal é um conceito superior (porque abrange extensionalmente o inferior) e homem é um conceito inferior (porque é abrangido extensionalmente pelo superior). Mas animal também tem um gênero. Em síntese, podemos dizer que: substância" é o genus generalissimum (O conceito mais superior de todos, aquele que não é abrangido por nenhum outro). "Corpórea" é uma espécie de "substância" e gênero de "corpo"; "corpo" é uma espécie de "corpórea" e gênero de "animado"; "animado" é espécie de "corpo" e gênero de "animal"; "animal" é espécie de "animado" e gênero de "racional"; "racional" é espécie de "animal" e gênero de "humano"; "humano" é espécie de racional e não é gênero dos homens particulares, é uma espécie que é apenas espécie, ou infima specie (Ou o conceito mais inferior, aquele conceito que não abrange nenhum outro conceito (Homens particulares não são conceitos, são indivíduos)).
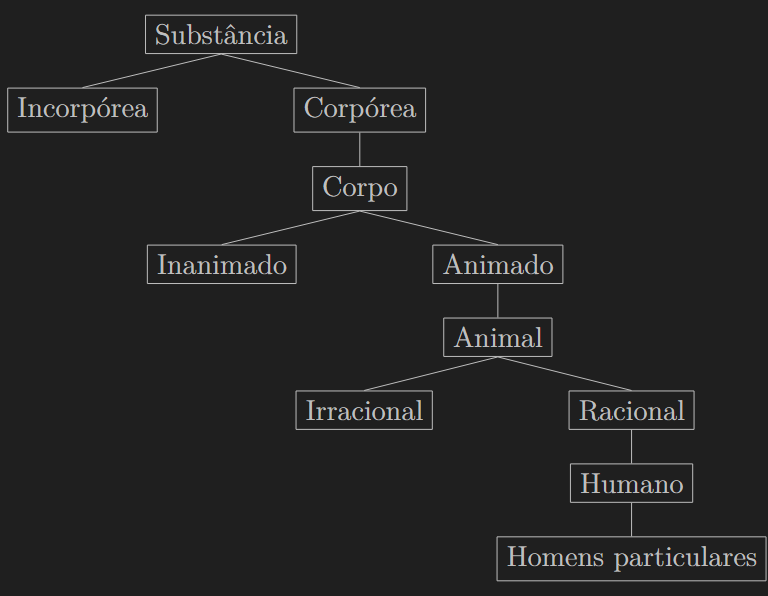
Leia atentamente à explicação acima enquanto compara com essa figura da Árvore de Porfírio.
As essências também têm distinções. A essência superior é a essência do gênero de dado conceito. Vamos pegar o termo homem. O gênero de homem é animal. A essência de animal (extraída da definição) é sensível (pois vem da definição: Organismo sensível), portanto, sensível é essência genérica de homem (já que o gênero de homem é animal e animal tem como essência ser sensível). A essência específica, por sua vez, é a essência da espécie, ela também é extraída da definição. A essência específica de homem é ser racional, pois a definição de homem é: Animal (gênero mais próximo) racional (diferença específica). Disso tudo, decorre que:
Em síntese:
Conceito superior: abrange extensionalmente o inferior.
Conceito inferior: é abrangido extensionalmente pelo superior.
Essência genérica: a essência do gênero do termo em questão. No caso do homem: sensível.
Essência específica: a essência da espécie do termo em questão. No caso do homem: racional.
O conceito é o produto da concepção, que é a primeira operação do intelecto. A concepção é o ato de formação do conceito operado pelo intelecto.
Existem diversos tipos de discursos práticos, são eles:
Discursos práticos:
Discurso dubitativo: aquele que interroga.
Exemplo: O que você almoçou ontem?
Discurso imperativo: aquele que ordena.
Exemplo: Me dê uma Coca-Cola!
Discurso suplicativo: aquele que pede.
Exemplo: Por favor, me dê uma Coca-Cola.
Discurso vocativo: Aquele que chama.
Exemplo: Ei! Guilherme!
Todos os discursos acima são de ordem prática, eles representam uma utilidade muitas vezes cotidiana, trivial, sem necessariamente uma relevância teórica.
Há, porém, um outro tipo de discurso: aquele que enuncia uma relação de conceitos. Damos um nome a esse discurso, o discurso enunciativo. É ele que forma a proposição.
Discurso enunciativo:
Todo homem é mortal.
Este aparelho é eletrônico.
João é um coelho.
Este discurso é falacioso.
O discurso enunciativo afirma uma imposição de ordem intelectual, ele impõe uma certa verdade na realidade. Dizer: "Sócrates é mortal" impõe a Sócrates um predicado, a saber, que ele é mortal. Disso, chegamos à Segunda Operação do Intelecto: O juízo.
Assim como o produto da concepção (primeira operação do intelecto) é o conceito. O produto do juízo (segunda operação do intelecto) é a proposição.
A proposição representa um juízo, ela assevera a relação entre conceitos. A asserção: "Sócrates é mortal" é o produto de um juízo, ela afirma a relação entre um sujeito e um predicado, através de uma cópula. A asserção "Sócrates é mortal", assim como toda asserção composta de sujeito, cópula e predicado que assevera a relação entre sujeito e predicado, é uma proposição.
Elementos de uma proposição:
Sujeito: Aquele sobre o que o algo é asseverado.
Exemplo: Sócrates é mortal.
Predicado: Aquele que é asseverado a respeito de algo.
Exemplo: Sócrates é mortal.
Cópula: Aquele que assevera a relação.
Exemplo: Sócrates é mortal.
A forma da proposição é a cópula, a sua matéria é o sujeito e o predicado.
É uma propriedade de todas as proposições serem ou verdadeiras, ou falsas.
A proposição é produto do juízo, segunda operação do intelecto. Juízo é o ato do intelecto pelo qual ele julga.
A terceira operação do intelecto é o raciocínio, onde da relação de outros conceitos, surge uma nova e inédita relação. É o ato do intelecto do qual ele alcança informações desconhecidas a partir de informações conhecidas. Seu produto é o argumento. Um raciocínio pode ser de descoberta ou de justificação, um raciocínio de justificação é aquele onde a conclusão já é sabida previamente e o ato de raciocínio é um meio de justificá-la. Já o de descoberta é o raciocínio puro, onde as premissas são conhecidas e a conclusão é desconhecida. Em síntese, podemos dizer que a primeira operação do intelecto é o entendimento da essência das coisas (concepção), a segunda operação é o entendimento da relação entre os conceitos das coisas (juízo) e que a terceira operação é o entendimento da relação das relações entre os conceitos das coisas (raciocínio).
Exemplo de raciocínio:
Maria é mãe de Jesus
Jesus é Deus
Logo, Maria é mãe de Deus.
O "salto" das premissas desconhecidas para a nova e inédita proposição é chamado de inferência.
O silogismo é o argumento por excelência, é a forma perfeita de argumentação. Um silogismo é um ato onde de duas proposições conhecidas (premissas) uma nova e inédita conclusão necessariamente decorre.
Matéria e forma do silogismo:
Matéria:
Matéria próxima: proposição maior e menor Matéria remota: termo menor, maior e médio.
Forma:
Modo: Disposição das proposições do silogismo conforme as formas AEIO.
Figura: Disposição dos termos do silogismo conforme a posição do termo médio.
Um silogismo tem sempre três termos: o termo menor, maior e o médio. O termo menor é o sujeito da conclusão, o termo maior é o predicado da conclusão, o termo médio é o termo que aparece nas duas premissas mas não aparece na conclusão, é o termo médio que estabelece um certo tipo de nexo entre as duas premissas e a conclusão, ele que é o elo do silogismo. Uma das regras do silogismo diz que o termo médio deve estar distribuído ao menos uma vez em alguma das duas premissas, como ficará claro mais para frente.
O termo menor será sinalizado por (t), o termo maior será sinalizado por (T), o termo médio será sinalizado por (m). A premissa menor é a premissa que contém o termo menor, a premissa maior é a premissa que contém o termo maior. Os grandes lógicos convencionaram que um silogismo deve sempre começar pela premissa maior, por fins de padronização de taxonomia.
Exemplo de silogismo:
Deus (t) é um ser perfeito (m).
Um ser perfeito (m) necessariamente existe (T).
Logo, Deus (t) existe (T).
A figura, como dito anteriormente, é determinada pela posição do termo médio no silogismo. Temos quatro figuras, são elas:
Figuras:
sub-prae:
É onde o termo médio é sujeito na premissa maior e predicado na premissa maior.
sub-sub:
O termo médio é sujeito em ambas as premissas.
prae-sub:
O termo médio é predicado na premissa maior e sujeito na premissa menor.
prae-prae:
O termo médio é predicado em ambas as premissas.
Um bom argumento pode assim ser dito se atualizar todas as potências que lhe são próprias. Isso quer dizer que bons argumentos devem ser bem formulados e devem seguir as regras da lícita argumentação. Quando um argumento não respeita as regras da lícita argumentação, dizemos que ele é inválido.
Diferença entre validade e veracidade: a validade é um predicamento de qualidade atribuído aos argumentos, a veracidade é um predicamento de qualidade atribuído às proposições. Um argumento é válido quando assumida a veracidade de suas premissas constituintes, a conclusão necessariamente se siga. Uma proposição é dita verdadeira quando o juízo representado por ela se segue na ordem da realidade.
Um argumento sempre tem como fim ou a justificação de uma tese, ou a descoberta de uma nova tese.
A corretude de um argumento é a implicação formal da conclusão relativamente às premissas verdadeiras que o constituem. Em suma, a soma das notas de validade com as notas de veracidade.
Signo: é tudo aquilo que aponta para alguma coisa, é tudo aquilo que tem uma espécie de intencionalidade. Tome como exemplo a palavra "elefante", a palavra "elefante" é um signo no sentido de que é um veículo verbal, é uma palavra.
Exemplo: palavras, pois elas são usadas para representar alguma outra coisa. Uma placa na rua é um signo porque ela chama a atenção para uma lombada, cruzamento ou coisa que o valha.
Significado: é aquilo que é representado imediatamente. No exemplo da placa, o conceito de lombada ou o conceito de cruzamento são exemplos de significados. O significado é um ente mental. O significado também pode ser interpretado como um outro conjunto de palavras que formam uma definição, um significado. Voltando no exemplo do elefante, a definição de elefante constitui o significado.
Referente: Aquilo que é representado mediatamente. No caso do exemplo da placa, a lombada real, presente em algum lugar da rua, ou o cruzamento real, presente em algum lugar da rua. Os referentes normalmente (mas não exclusivamente) são entes reais. No exemplo do elefante, o referente é o próprio elefante real.
Você deve ter visto a presença do termo categoremático de relação mediatamente e imediatamente presente nas definições apresentadas, para entender isso, vamos tomar como referencial o signo: o signo representa o significado, ele "aponta" diretamente para o significado, logo, o significado é representado imediatamente pelo signo. Agora vamos para o referente: o referente está mais próximo do significado, isto é, mais próximo do conceito de si mesmo do que sua representação puramente verbal (palavra), logo, o signo representa mediatamente (esta relação mediata é mediada pelo significado) o referente. O signo é um ente verbal, normalmente uma palavra. O significado é normalmente um ente mental, um conceito ou coisa do gênero. O referente é algo real, aquilo a que o signo aponta mediatamente. Uma placa de trânsito é um signo, o seu significado é o conceito de lombada, a lombada mesma é o referente, o ente real a que o signo aponta mediatamente e do qual o significado é o conceito. Deste modo, podemos sintetizar com:
Resumo:
Signo: tudo aquilo que representa outra coisa. (ente verbal).
Significado: aquilo que é representado imediatamente. (ente mental).
Referente: aquilo que é representado mediatamente. (ente real).
Algumas palavras podem ser homônimas ou sinônimas. Elas são homônimas quando a palavra tem a mesma matéria mas se referem a coisas diferentes, é quando o acordo de palavra é idêntico, mas ocorre uma discrepância de significado. Por exemplo: eu posso entender como imoral um conjunto x de comportamentos imorais, já você, pode entender por um conjunto y de comportamentos imorais, ou ainda pior: você pode entender esse conjunto como tendo propriedades completamente diferentes do meu, isso significa que nós estamos usando a mesma palavra, mas com significados completamente diferentes. Já as palavras sinônimas é quando há acordo de grafia e significado, é quando nós usamos a mesma palavra para se referir ás mesmas coisas. "Homônima" é traduzida muitas vezes para "homonímia" ou palavra ou termo "equívoco". Já a "sinônima" é traduzida muitas vezes para "sinonímia" ou palavra ou termo "unívoco". Use o que achar melhor.
Para definir as homônimas e sinônimas, nós usamos o termo "termo". Mas o que é um termo, afinal? Um termo é a representação verbal de um conceito, um termo sempre se refere a um e apenas um conceito, isso significa que todo termo deve necessariamente ser unívoco (apenas neste sentido). A diferença entre uma palavra e um termo é que uma palavra tem vários significados em potencial, um termo já tem um e apenas um significado designado e atualizado. Tenha sempre em mente que um termo é a expressão verbal de um conceito.
O nosso esquema de signo
A definição é um meio de garantir a perfeição da primeira operação do intelecto, é uma forma de ter certeza que o conceito que temos sobre algo é adequado. "Definir" é delimitar os fins. É expressar a essência de um conceito, mostrar sua intenção. Em síntese:
Definição:
Definir é o ato de explicitar a intensão de um conceito.
A definição lógica é uma espécie de definição rigorosa. Ela é dada por: [gênero mais próximo] + [diferença específica]. A diferença específica também foi chamada de essência específica, são a mesma coisa. A definição lógica é sempre de uma espécie, a coisa por se definir é sempre uma espécie de algo. Por exemplo: homem [espécie] é um animal [gênero mais próximo3] + [diferença específica]. Na definição lógica, designamos uma classe e posteriormente aquilo que designa a espécie por se definir, chamo atenção novamente para a definição de homem.
Regras de uma definição:
Regra da exaustividade: uma definição deve abranger toda a intensão e extensão de um conceito.
Uma definição deve ser exaustiva no sentido de que designe um e apenas um elemento de um conjunto. A definição "animal racional" é excelente porque apenas uma coisa nesse mundo é designada por ela, a saber, os seres humanos. Disso decorre a segunda regra.
Regra da exclusividade.
A definição deve abranger somente a intensão e a extensão da coisa definida.
A fórmula da definição lógica é excelente porque com a designação do gênero mais próxima, cumprimos com a primeira regra, com a diferença específica, cumprimos a segunda regra.
Regra da clareza.
Não se pode pressupor um conhecimento prévio do termo por se definir, isto é, não posso definir algo com relação à espécie por se definir. Por exemplo: não se pode definir "vetor" por "elemento do campo vetorial". Ora, se o termo por se definir encontra-se desconhecido, como posso usá-lo com um tipo de flexão? Isso constitui numa definição circular e inadequada. Uma definição é inadequada quando fere alguma regra das definições.
Regra da negatividade.
A definição não pode ser negativa. A definição, por definição exprime a quidade de alguma coisa. Definir algo em termos do que ela não é é algo que torna uma definição inadequada, assim como a quebra de qualquer outra das regras de definição.
A divisão é o ato de distribuir um todo em suas partes. É interessante dividir conceitos no sentido de que o ato de dividir nos traz um entendimento particularizado do conceito. Dividir um conceito o torna mais claro e mais facilmente assimilável. Por exemplo: Movimento é deslocamento ou alteração. Podemos dizer que a definição de um conceito é uma análise de sua intensão, enquanto a divisão lógica é uma análise de sua extensão.
Todo, partes e base: o todo é aquilo que é dividido, muitas vezes chamado de dividendo. As partes são o produto dessa divisão, muitas vezes chamado de quociente. A base da divisão é a razão da divisão, o critério usado para dividir. Tome como exemplo uma biblioteca, a divisão dos livros dessa biblioteca tem como base, suponhamos, o gênero dos livros. O todo é a biblioteca mesma, o conjunto de todos os livros presentes nela. A base é o gênero dos livros. As partes são os setores de filosofia, matemática, etc.. Em síntese:
Resumo:
Todo: aquilo que é dividido.
Parte: aquilo que é o produto da divisão.
Base: a razão ou critério da divisão
Assim como a definição, a divisão tem uma fórmula, ela é:
Divisão lógica: [gênero] é [espécies]
Regras da divisão:
Regra da exaustividade: o produto da divisão deve exaurir o todo.
Isso significa que as partes devem ser coletivamente exaustivas, isto é, contemplar a totalidade do todo. No nosso exemplo da biblioteca, não seria adequado dividir os livros só em setores de filosofia, pois na nossa biblioteca também tem livros de ficção, teologia, etc., portanto, isso feriria a nossa primeira regra.
Regra da exclusividade: o produto da divisão deve excluir as partes do todo entre si. (mútua exclusividade)
Isso significa que não se pode ter intersecções entre os produtos da divisão. Por exemplo: não podemos ter um setor em uma biblioteca que seja de livros azuis e livros de filosofia pois aí haveria um tipo de intersecção entre as partes e isso não pode acontecer, alguns livros seriam de filosofia mas não seriam azuis, outros seriam azuis mas não seriam de filosofia, isso cria uma ilícita intersecção entre os conjuntos-produto.
Regra da base: a divisão deve ter uma base comum.
Vamos voltar ao nosso exemplo da biblioteca, nós não poderíamos dividir a biblioteca em livros azuis, livros vermelhos, livros de filosofia e livros de matemática, pois nos dois primeiros exemplos, a base é a cor, nos dois últimos, a base é o gênero.
Regra da extensão: O produto da divisão deve ser maior do que as partes.
Não poderíamos dividir a biblioteca de forma que os setores somassem uma maior quantidade de livros do que há na biblioteca inteira, tampouco faria algum sentido ter um setor que tem a exata mesma quantidade de livros do que na biblioteca inteira. As partes sempre devem ser menor que o todo.
A divisão é um movimento evidentemente descendente, seu equivalente oposto seria a classificação, que tem como movimento naturalmente ascendente. Se eu quisesse classificar o conjunto que contém a espécie humana, eu ascenderia ao gênero animal, mas animal é uma espécie de ser vivo, então, caso eu queria classificar ainda mais adiante, ascenderia ao gênero ser vivo. Se, portanto eu quisesse classificar mais ainda, ascenderia ao gênero corpórea, até chegar no gênero supremo "substância". A classificação é o ato de ascender da parte ao todo.
Desta forma, fica claro que a divisão é descendente e a classificação é ascendente.
Para elucidar o conceito de subdivisão, tomemos novamente o exemplo da Árvore de Porfírio que tem como gênero supremo a substância e como espécie ínfima a humana. Vamos tomar o gênero animal, caso eu queira distinguir dentre os animais segundo o critério de alado, aquático ou terrestre, eu estaria fazendo algo que é chamado de subdivisão. No gênero animal, eu já tenho duas espécies, a saber: racional e irracional, se, portanto, quiséssemos dividir a espécie irracional entre alado, aquático e terrestre, este ato é o que chamamos de subdivisão. Deste modo, fica claro que a subdivisão é uma divisão subordinada a uma precedente.
A codivisão é uma série de divisões de um mesmo todo com bases diferentes. Distinguir os animais irracionais entre alados, verdes, bípedes e sem pelagem é um tipo de codivisão, pois a divisão é de um mesmo todo, a saber: os animais irracionais. Esta divisão é feita com diferentes bases, a saber: alado, verde, bípede e sem pelagem. A codivisão não pode ser simultânea, isto é, para usar bases diferentes, devemos dividir conforme uma dada base e depois desfazer a divisão. Só após de desfeita a divisão prévia é que podemos usar uma base diferente. Deste modo, podemos sintetizar o que foi dito com:
Resumo:
Classificação: O ato de ascender da parte ao todo.
Subdivisão: Divisão subordinada a uma precedente.
Codivisão: Série de divisões de um mesmo todo com bases diferentes em cada divisão individual.
Na doutrina das divisões e das classificações, chegou-se num problema: poderíamos nós, chegarmos em algum limite, algum "teto"? Já sabemos que essa classificação não pode ser infinita, pois isso seria absurdo. Sabemos também que essa classificação, se feita perfeitamente, há necessariamente um início, ou um "piso". Qual seria, então, os tetos e os pisos? Aristóteles chegou na resposta de que todas essas coisas se subordinam a dois grandes gêneros: substância e acidentes. A substância é tudo aquilo que existe por si só: eu, você, uma planta, uma mesa, uma cadeira, etc.. Acidente é tudo aquilo que existe em uma substância: a cor das coisas, o ato de pensar, o ato de correr, o ato de estar vestido, a relação das coisas umas com as outras, etc.. Aristóteles também percebeu que todas as palavras que significam algo por si só podem ser reduzidas a esses gêneros do ser.
Disso temos:
Gênero supremos:
Gêneros supremos (Predicamentos): são os gêneros de todas as coisas que não são espécies de nenhum gênero.
Substância é a essência mesma do ser, é aquilo que faz o ser ser o que ele é, é algo constitutivo da coisa.
Dentro dos acidentes, temos nove. Contando com a substância, contam-se dez predicamentos, são eles:
Em síntese:
Substância é o ente que existe em si mesmo.
Exemplo: homem, filósofo, político, eu, você, esta coisa, aquela coisa, etc.
Quantidade: é uma determinação dos pontos materiais da substância enquanto mensuráveis.
Exemplos: um metro e noventa, cento e vinte e nove quilos, oitenta e oito arrobas, etc.
Qualidade: é uma determinação da natureza de uma substância.
Exemplo: gramático, preto, filosófico, poético, teológico, etc.
Relação: é uma referência que uma substância ou acidente estabelece com outro.
Exemplo: conhecimento4, maior, menor, grande5, pequeno, etc.
Convém fazer uma pequena pausa para aprofundar um pouco na relação, já que este é um predicamento muito abusado nos dias de hoje. Para que algo seja relação, deve necessariamente ter três termos:
Sujeito: Aquele que tem uma determinada relação.
Termo: aquele com quem tem determinada relação.
Base: O fundamento dessa relação.
Tomemos como exemplo a relação de mãe e filho. O sujeito da relação é o filho, o termo é a mãe e a base é a maternidade. Depois dessa breve divagação, passemos para o restante:
Ação: é o exercício da substância que produz um efeito.
Exemplo: queimar, pensar, correr, fugir, etc.
Paixão: é a recepção da substância de um efeito produzido por um agente.
Exemplo: ser queimado, ser pensado, ser cortado, etc.
Quando: posição em relação ao curso de eventos extrínsecos.
Exemplo: ontem, amanhã, depois, mais tarde, etc.
Onde: é a posição em relação aos corpos que circulam uma substância.
Exemplo: em casa, no Liceu, etc.
Postura: é a posição que certos pontos da substância têm quanto às outras e vice-versa.
Exemplo: sentado, prostrado, etc..
Estado: é a condição que distingue um indivíduo de outros.
Exemplo: calçado, vestido, cortado, morto, etc.
Espécie ínfima: o "piso" da classificação consiste nas espécies ínfimas, que são as espécies onde abaixo delas só hão indivíduos, "homem" é um exemplo de espécie ínfima, pois abaixo da espécie humana, só há os seres humanos individuais propriamente ditos.
O argumento é um produto da terceira operação do intelecto, que é o raciocínio, ele mostra uma relação de relações de conceitos. A formação da relação de conceitos é operada pela segunda operação do intelecto, o juízo. O juízo forma o que nós chamamos de relações de conceitos. Os conceitos, por sua vez, são obra da primeira operação do intelecto, a concepção, onde a inteligência abstrai a realidade a partir de um indivíduo, de forma a isolar aquilo que lhe é essencial. A imperfeição na primeira operação do intelecto leva a um problema grave, que é a violação das regras do silogismo. A regra 1 diz que podemos ter três e apenas três termos. Quando usamos termos com significados diferentes mas com a grafia idêntica, caímos na violação da primeira regra do silogismo, aqui está um exemplo:
Exemplo:
Depilação não é imoral.
Ora, depilação é antinatural.
Logo, algo antinatural não é imoral.
Perceba que o termo "antinatural" foi usado em acepções diferentes, ora referindo-se àquilo que é antinatural somaticamente, ora referindo-se àquilo que é antinatural teleologicamente. Nesse caso, dizemos que há quatro termos, o silogismo usado como exemplo é inválido.
Uma segunda regra é a de que um silogismo deve conter três e apenas três proposições. A violação desta regra é a falácia das quatro proposições.
Deste modo, temos as primeiras duas regras do silogismo:
Em síntese:
Um silogismo deve ter três e apenas três termos.
Um silogismo deve ter três e apenas três proposições.
Agora que estamos familiarizados com as duas primeiras regras do silogismo, cabe apresentar um novo argumento:
Silogismo:
Deus é um ser perfeito.
Um ser perfeito necessariamente existe.
Logo, Deus existe.
Esse argumento pode parecer funcional à primeira vista, mas ele tem um problema: perceba que na primeira proposição, "Deus" é tratado como se fosse um conceito, isto é, mesmo para alguém ateu, essa premissa é impossível de falsear, pois o conceito de deus necessariamente é perfeito. Já na segunda premissa, "um ser perfeito" é usado como que fazendo referência à realidade, essa transição da dimensão conceitual para a dimensão real do significado do termo é algo ilícito, não pode acontecer porque é falacioso. Mas qual é o problema desse argumento?
O problema desse argumento é análogo a esse próximo silogismo:
Flor é irracional.
Maíra é uma flor.
Logo, Maíra é irracional.
Perceba que neste silogismo, a premissa maior explora um conceito mais literal predicando irracional de flor. Porém, na premissa menor, "Flor" já é usada com referência não a seu significado literal, mas analógico. Perceba que o termo "flor" foi usado com referências a dimensões distintas da realidade, ora como literal, ora como analógica. À essa troca de sentido, damos o nome de suplência. É correto dizer que no silogismo usado como exemplo, o termo "flor" está sendo usado em suplências diferentes. Desta breve explicação, chegamos à seguinte definição:
Suplência: função que um termo possui de substituir uma coisa no discurso.
Dizemos que a suplência de um termo é a capacidade que um termo tem de ocupar o lugar de alguma coisa real. No silogismo-exemplo, traduziríamos isto para "a capacidade que o termo "flor" tem de ocupar o lugar de uma flor real no discurso". Existem diversos tipos de suplências, estudaremos todos eles na seguinte seção. Sempre que nos referirmos a suplência de alguma coisa, estaremos nos referindo a suplência de um termo. Os entes de razão que possuem suplência são termos.
Quando um termo é usado para referir-se a si mesmo, dizemos que ele tem suplência material, isto é, o termo supre sua função enquanto palavra de forma reflexiva.
Exemplo: ""Deus" tem quatro letras"
Repare que aqui a palavra "Deus" é usada somente enquanto signo verbal, sem apontar para seu significado.
Já na suplência formal, dizemos que o termo supre sua função pelo seu significado ou referente. Um exemplo disso seria a proposição: "Pedro é homem". Repare que aqui os termos são usados com referência a seu significado, apontando para seu significado mesmo ou referente. Neste caso, dizemos que a suplência é formal.
Uma outra possível divisão de suplência, já admitindo que todas as suplências envolvidas são formais é a seguinte: podemos nos referir apenas ao significado, sem nos referir aos referentes, como quando dizemos: "Deus é um conceito universalmente conhecido". Bem como podemos também usar um termo como que referindo-nos tanto a seu significado quanto aos seus referentes, como quando dizemos "Deus é um ser perfeito". Nesse caso, perceba que "perfeito" predica-se tanto do conceito de Deus como Deus enquanto coisa real, neste caso, dizemos que a suplência é pessoal, pois se deus se materializasse na nossa frente agora mesmo, poderíamos tranquilamente dizer: "Este é um ser perfeito". Já no outro exemplo, não faria sentido dizer ao referente Deus algo como: "Este ser é um conceito universalmente conhecido", pois entes reais não são conceitos. Nosso primeiro exemplo - o de que Deus é um conceito universalmente conhecido - constitui uma suplência impessoal, o segundo - o de que Deus é um ser perfeito - constitui suplência pessoal. Podemos, entretanto, suprir também pelo referente apenas, este é o caso da suplência discreta, a suplência discreta tem sempre como matéria nomes, substantivos próprios. Um exemplo de suplência discreta seria "Sócrates", "Platão", "Guilherme", etc.
Podemos também usar suplências próprias e impróprias. Uma suplência própria é quando o termo é usado para representar aquilo que ele normalmente representa. Por exemplo: "Flores têm pétalas". Já a suplência imprópria é quando um termo é usado segundo um significado metafórico ou metalinguístico. Por exemplo: "Maíra é uma flor". Tanto a suplência própria quanto a imprópria estão contidas na suplência formal.
Já dentro das suplências pessoais, temos a suplência parcial, coletiva e total. Nessas três caracterizações, tomamos a suplência pessoal do ângulo da extensão do termo. Um exemplo de suplência total seria o de que "Todos os homens são mortais", pois podemos predicar de cada homem o predicado "mortal". Um exemplo de suplência coletiva seria a de que "Os apóstolos eram doze", veja que não podemos predicar de cada apóstolo individual o predicado "doze", pois eles representam doze enquanto coletivo, não enquanto indivíduos. Por fim, a suplência parcial é quando um termo é usado em parte da extensão como que em "Alguns homens são calvos".
Quando a suplência é total, pode suprir de formas diferentes. Quando dizemos "Todo homem é mortal", naturalmente intuímos de que isso se predica de todo e qualquer homem. Mas se dizemos, por exemplo: "Todos os animais estavam na arca de Noé", seu cachorro claramente não estava, portanto, o predicado dessa proposição não se aplica ao seu cachorro. No primeiro exemplo e no segundo, os termos têm suplência total, mas eles diferem em modo, porque no segundo exemplo a suplência é distributiva, mas não por todos indivíduos e sim por todas as espécies que estão contidas na extensão do termo. Podemos ainda suprir de modo exceptivo, que é quando a suplência é total mas admite exceções pontuais. Por exemplo: "Todo homem é pecador" admite exceções, a saber, Jesus Cristo, mas o termo ainda supre totalmente as espécies.
Agora, em outro tipo de suplência, temos a determinada e a confusa. Quando dizemos: "Pedro é calvo’, determinamos Pedro e em seguida atribuímos-lhe um predicado. Agora, se dissermos "Algum homem é calvo", veja que não há determinação individual, os referentes existem, mas não são indeterminados.
Vamos agora apresentar uma tabela com as definições de cada tipo de suplência junto com um exemplo em cada um deles:
Suplência material: termo supre pelo signo.
Exemplo: "Doce" é um adjetivo.
Suplência formal: termo supre pelo significado ou referente.
Exemplo: Deus é um ser perfeito.
Suplência imprópria: termo supre pelo significado impropriamente.
Exemplo: Maíra é uma flor.
Suplência própria: termo supre pelo seu significado propriamente.
Exemplo: Flores têm pétalas.
Suplência impessoal: termo supre apenas pelo conceito que significa imediatamente.
Exemplo: Deus é um conceito interessante.
Suplência pessoal: termo supre pelo seu significado imediatamente e pelos referentes que significa mediatamente.
Exemplo: Deus é onipotente.
Suplência discreta: termo supre apenas pelo referente.
Exemplo: Sócrates6 é mortal.
Suplência parcial: termo supre por parte da extensão.
Exemplo: Algum animal é racional.
Suplência coletiva: termo supre por tudo que significa tomado coletivamente.
Exemplo: Os apóstolos são doze.
Suplência total: termo supre por tudo que significa tomado distributivamente.
Suplência completa: supre por todos indivíduos da extensão.
Exemplo: Todo homem é mortal.
Suplência incompleta: supre por todas as espécies da extensão (gênero).
Exemplo: Todos os animais estavam na arca de Noé.
Suplência exceptiva: supre por toda a extensão, mas admitindo exceções.
Exemplo: Todo homem é pecador.
Suplência determinada: termo supre pelos seus referentes determinados.
Exemplo: Pedro é calvo.
Suplência confusa: termo supre pelo seus referentes indeterminadamente.
Exemplo: Alguém é calvo.
A distribuição é uma propriedade fundamental dos termos quanto a se são usados em toda a sua extensão ou não. Uma proposição total é como a "Todo homem é mortal" e tem seu sujeito distribuído em toda a extensão. Uma proposição parcial como a "Algum homem é mortal" tem seu sujeito não distribuído em toda sua extensão, pois apenas parte dos referentes do conceito homem estão sendo designados. A quantidade de uma proposição pode ser total ou parcial.
Porém, para chegarmos à distribuição do predicado, devemos considerar a qualidade da proposição, que pode ser negativa ou afirmativa. As proposições afirmativas têm seu predicado não distribuído, pois o predicado normalmente é um termo que possui maior extensão e também porque só uma pequena quantidade do conceito do predicado (a saber, a parte que é predicada do sujeito) é designada. Uma proposição afirmativa é como a "Jesus é Deus". Proposições negativas têm seu predicado distribuído, pois o predicado exclui o sujeito de toda a sua extensão, proposições como "Pedro não é calvo" são proposições negativas. A qualidade de uma proposição pode ser ou afirmativa ou negativa.
Em proposições singulares, como "Jesus cumpriu com as profecias" devemos assumir que sua quantidade é total, pois o sujeito, normalmente um indivíduo, é designado em sua extensão (nesse caso, de Jesus predica-se que cumpriu com as profecias). Uma proposição como a do exemplo é uma singular indefinida, uma proposição pode ter como natureza tanto singular quanto geral. Uma proposição geral pode ser como "Um triângulo tem três lados", bem como a proposição "O homem é mau". A distribuição do sujeito das proposições gerais pode ser um pouco variável, pois depende da intenção em que foi utilizada, na proposição "Um triângulo tem três lados", podemos facilmente intuir que quem fez esse juízo quis se referir a todos os triângulos. Mas na proposição "O homem é mau" isso já não é mais tão claro, mesmo que essa também seja uma proposição geral. Posso tentar explorar conceitos diversos nessa proposição, posso querer explorar um conceito um pouco mais próximo de como na proposição "O homem frequentemente é mau", e nesse caso essa proposição teria seu sujeito não distribuído, pois o homem frequentemente (parcial) é mau, mas nem sempre (total). Bem como poderia ter explorado o conceito de que, definicionalmente, o homem é intrinsecamente mau, e nesse caso o sujeito seria distribuído, portanto, nas proposições gerais, isso já não é mais tão claro e deve ser decidido com base no contexto e na intenção que o locutor intendeu.
Em síntese:
Proposição total (Quantidade): distribui seu sujeito em toda a extensão. (d)
Exemplo: (Todo) homem é mortal.
Proposição parcial (Quantidade): não distribui seu sujeito em toda extensão. (nd)
Exemplo: (Alguns) homens são mortais.
Proposição afirmativa (Qualidade): não distribui seu predicado em toda a extensão. (nd)
Exemplo: Cristo (é) rei.
Proposição negativa: (Qualidade): distribui seu predicado em toda a extensão7. (d)
Exemplo: Rex (não é) um homem.
Proposição singular: (Natureza): distribui sujeito em toda a extensão. (d)
Exemplo: (Pedro) é calvo
Proposição geral: (Natureza): a depender do contexto e intenção do locutor, pode tanto distribuir como não distribuir o sujeito. (?)
Exemplos: Um triângulo tem três lados / O homem é mau8.
Nós podemos determinar uma notação conveniente para os modos das proposições, é a forma AEIO. Para começar, tome como exemplo as duas palavras latinas: affirmo e nego, perceba que as duas primeiras vogais de affirmo são as letras "a", e "i", e na segunda palavra, "e" e "o", affirmo significa literalmente "eu afirmo", e nego significa literalmente "eu nego", as proposições A e I sempre têm então qualidade afirmativa9, e as proposições E e O, sempre negativas10. Quanto à qualidade, pode ser tanto total ou parcial. Para entender a notação, tome como "[S]" o sujeito, "(d)" como sinalizando que o termo está distribuído em toda a extensão, "(nd)" como sinalizando que o termo não está distribuído em toda a extensão e "[P]" como o predicado. A notação "S a P" significa "A proposição de modo A que tem S como sujeito e P como predicado", a notação "S i P" significa "A proposição de modo I que tem S como sujeito e P como predicado", a vogal que ficar entre as letras será usada para sinalizar o modo da proposição. Apresentaremos um pequeno quadro ilustrativo:
Em síntese:
(A) Total afirmativa: Todo padre é ordenado. [S(d)] a [P(nd)]
(E) Total negativa: Nenhum padre é ordenado. [S(d)] e [P(d)]
(I) Parcial afirmativa: Algum padre é ordenado. [S(nd)] i [P(nd)]
(O) Parcial negativa: Algum padre não é ordenado. [S(nd)] o [P(d)]
O termo médio de um silogismo deve estar distribuído em ao menos uma premissa do silogismo, essa é a chamada Regra III. Disto, temos que:
Um silogismo deve ter três e apenas três termos.
Um silogismo deve ter três e apenas três proposições.
O termo médio deve ser distribuído em toda sua extensão ao menos uma vez.
As formas AEIO dizem respeito somente à quantidade e qualidade das proposições, não levando sua natureza em consideração. No caso de proposições singulares indefinidas, o comportamento se identifica com os das proposições totais no sentido de ter o sujeito sempre distribuído, se for geral indefinida, variará de acordo com a intenção do locutor.
Tome como exemplo o silogismo seguinte:
Tudo do que se pode ter certeza é verdadeiro.
Ora, o mundo exterior não é certo.
Logo, não é verdadeira.
Aplicando as regras já vistas do silogismo, chegamos que é um silogismo sob o modo AEE, de termo menor "mundo exterior", termo maior "verdadeiro", e termo médio "certo" ou "certeza"11. Faremos agora como análise desse silogismo:
Tudo do que se pode ter certeza [M(d)] é verdadeiro [P(nd)].
Ora, o mundo exterior [S(d)] não é certo [M(d)].
Logo, (o mundo exterior) [S(d)] não é verdadeiro [P(d)].
Modo: AEE.
Perceba que este silogismo cumpre perfeitamente com a regra três, mas ele tem mais um problema: perceba que o termo "verdadeiro" está não distribuído em sua premissa mas está distribuído na conclusão, esta é uma falácia do processo ilícito, que quebra Regra 4 do silogismo, veremos a regra 4 mais à frente. Resumidamente, um termo não pode estar distribuído na conclusão caso ele não tenha sido distribuído na própria premissa. Portanto, o silogismo dado como exemplo é inválido. Tenha em mente que é necessário que todo termo que está distribuído na conclusão esteja distribuído na sua respectiva premissa, mas a inversa não se segue, pois caso um termo não esteja distribuído na conclusão, em nada lhe é exigido que esteja distribuído em sua respectiva premissa. A falácia é cometida apenas quando um termo está distribuído na conclusão mas não está na sua própria premissa.
É extremamente importante entender como podemos predicar determinadas coisas de outras, uma área da lógica que se propõe a estudar os modos de predicação é a área dos predicáveis.
Perceba que em toda forma de predicação, há uma espécie de relação que o predicado tem com o sujeito. Tome como exemplo o seguinte: enunciar "Maíra é humana" e enunciar "Maíra é dotada de linguagem articulada" são coisas distintas porque essas duas proposições diferem em modo de predicação, a presente aula pretende esclarecer o modo em que as diversas predicações podem se dar. Ilustraremos com o seguinte exemplo:
Gênero:
Maíra é animal.
Perceba que neste modo de predicação, dizemos que o sujeito está contido numa determinada classe e que essa mesma classe abrange outras coisas. Essa predicação é a que chamamos de gênero, pois dizemos que Maíra é do gênero animal e que isso de certa forma constitui algo de Maíra. Vamos agora para o próximo exemplo:
Espécie:
Maíra é humana.
Perceba que aqui também dizemos que o sujeito é abrangido por um tipo de classe, mas que agora essa classe não abrange tantos indivíduos como o exemplo anterior, essa predicação enuncia a espécie de Maíra, algo que veremos mais à frente. Dito isso, podemos partir para o próximo exemplo:
Diferença específica:
Maíra é racional.
Perceba que nesta predicação, não dizemos que o sujeito pertence a uma classe, mas sim que possui um atributo e que toda a classe que ela imediatamente está inserida também o possui. Dizemos que essa forma de predicação diz respeito a diferença específica, que também veremos mais à frente. Agora, para o próximo exemplo:
Propriedade:
Maíra é dotada de linguagem articulada.
Perceba que neste exemplo, trata-se de predicar algo que não é necessariamente essencial de Maíra, isto é, não precisamos que Maíra seja dotada de linguagem articulada para que se identifique com a própria existência. Estamos diante de um predicável de propriedade, que é quando algo deriva da essência do sujeito, mas que não necessariamente se identifica com ela. Ao próximo exemplo:
Acidente: Maíra é loira.
Perceba que neste caso, o predicado é perfeitamente dispensável, é algo puramente acessório de Maíra ser loira, pois ela poderia perfeitamente pintar o cabelo e ainda assim sua se identificaria com a própria existência. Estamos diante de uma predicação acidental.
Perceba, antes de apresentarmos a tabela, que todo e qualquer conceito cairá sobre algum desses modos de predicação; ou será gênero, ou espécie, ou diferença específica, ou propriedade ou acidente.
Em síntese:
Gênero: aquilo que é predicado necessária, constitutiva, parcial e indeterminadamente de algo.
Exemplo: Maíra é animal.
Espécie: aquilo que é predicado necessária, constitutiva e totalmente de algo.
Exemplo: Maíra é humana.
Diferença específica: aquilo que é predicado necessária, constitutiva, parcial e determinadamente de algo.
Exemplo: Maíra é racional.
Propriedade: aquilo que é predicado necessária mas não constitutivamente de algo.
Exemplo: Maíra é dotada de linguagem articulada.
Acidente: aquilo que é predicado contingencialmente de algo.
Exemplo: Maíra é loira.
Voltando ao exemplo do:
Corruptível é aquilo que tem partes que podem ser divididas até a destruição.
Ora, o corpo é algo que tem partes que podem ser divididas até a destruição.
Logo, o corpo é corruptível
Já adianto que o problema não se encontra nas regras que já foram apresentadas, pois elas são impecáveis. Lembre-se que este silogismo é inválido segundo as regras que nós já conhecemos, então o problema só pode estar na nossa prudência ao aplicar essas regras.
Dentre os predicáveis12 existe uma divisão a ser feita, isto é, entre as que são necessárias e as que são contingentes. Sendo necessárias podem ser totais ou parciais, e sendo parciais, podem ser de forma determinada ou de forma indeterminada. Dentro do que é contingente, temos o acidente; dentro do que é necessário mas não constitutivo, temos a propriedade; dentro do que é necessário, constitutivo e total, temos a espécie; dentro de necessário, constitutivo, parcial e determinado, temos a diferença específica; dentro do que é necessário, constitutivo, parcial e indeterminado, temos o gênero.
Voltando ao silogismo-exemplo mostrado no início da seção, a nossa prudência falhou no seguinte ponto: uma definição13 sempre distribui o seu predicado em toda a extensão. Ora, mas por quê? Digo-lhe; pois o sujeito da definição e seu predicado acabam por se identificarem em extensão e intensão, o motivo disto é evidente, pois aquilo que está sendo definido não é nada mais que sua definição abreviada. Portanto, o nosso silogismo não quebra nenhuma regra pois sempre que uma proposição for uma definição, terá tanto seu sujeito como predicado sempre distribuídos em toda a extensão.
Para finalizar o sistema de regras do silogismo, tome o seguinte silogismo como exemplo:
Todo disciplinado é constante.
Todo constante alcança seus objetivos.
Logo, alguns que alcançam seus objetivos não são disciplinados.
Este silogismo está com as regras de distribuição todas cumpridas.
Entretanto, a conclusão contraria o que se seguiria normalmente das premissas, tanto em qualidade quanto em quantidade. Portanto, precisamos de uma nova regra que supre a necessidade de diagnosticar esses silogismos como inválidos.
Regra 5: Um silogismo não pode ter uma conclusão negativa tendo duas premissas afirmativas.
À esta regra adicionamos que "De premissas gerais, não se tiram conclusões singulares". Via de regra, não podemos predicar indivíduos de coisas.
Para ilustrar o próximo exemplo, tome este silogismo:
O método dedutivo é o mais certo e rigoroso.
Algumas ciências não usam o método dedutivo.
Logo, a ciência não é certa e rigorosa.
Quando temos uma premissa fraca (prop. parcial ou negativa), a conclusão deve ser sempre condizente com ela. Ou seja, se uma premissa for parcial, então a conclusão também será parcial. Se a premissa for negativa, então a conclusão também será negativa.
Disto, temos a seguinte regra:
Regra 6: A conclusão deve sempre seguir as premissas mais fracas. A conclusão deve sempre seguir a premissa singular (se as duas premissas não forem singulares (Vide. silogismo expositivo: Aula 22)).
Para ilustrar o que se segue, tome o exemplo:
A maioria dos matemáticos são bons lógicos.
A maioria dos bons lógicos são filósofos.
Logo, a maioria dos matemáticos são filósofos.
Esse silogismo é inválido, nenhum termo está distribuído, mas ele é útil para explicitar a nossa próxima regra.
Regra 7: um silogismo não pode ter duas premissas fracas de mesma espécie.
Deste modo, podemos passar à tabela das regras do silogismo e suas violações respectivas:
Regras do Silogismo:
Um silogismo deve conter três e apenas três termos.
Violação: Falácia dos quatro termos.
Um silogismo deve conter três e apenas três proposições.
Violação: Falácia das quatro proposições.
O termo médio deve estar distribuído em pelo menos uma das premissas.
Violação: Falácia do termo médio não distribuído.
Se o termo menor ou maior estiver distribuído na conclusão, deverá estar também distribuído em sua respectiva premissa.
Violação: Falácia do termo menor ou maior não distribuído.
Um silogismo não pode ter uma conclusão negativa tendo duas premissas afirmativas. Um silogismo não pode ter uma conclusão singular tendo duas premissas gerais.
Violação: Falácia da conclusão mais fraca.
A conclusão deve sempre seguir as premissas mais fracas. A conclusão deve sempre seguir a premissa singular (se as duas premissas não forem singulares). Todas as fraquezas deverão ser seguidas.
Violação: Falácia da conclusão mais forte.
Um silogismo não pode ter duas premissas fracas de mesma espécie.
Violação: Falácia das duas premissas fracas.
| Categorias | Admite contrários? | Admite gradação? |
|---|---|---|
| Substância | Não | Não |
| Quantidade | Não | Não |
| Relação | Sim | Sim |
| Qualidade | Sim | Sim |
| Tempo | Não | Não |
| Lugar | Sim | Não |
| Estado | Não | Não |
| Ação | Sim | Sim |
| Paixão | Sim | Sim |
| Hábito | Sim | Sim |
| Predicáveis | Admite contrários? | Admite gradação? | Enuncia a essência? |
|---|---|---|---|
| Gênero | Sim | Não | Sim |
| Espécie | Sim | Não | Sim |
| Diferença | Sim | Não | Sim (Dif. específica) |
| Propriedade | Sim | Não | Não |
| Acidente | Sim | Não | Não |
Definições dos predicáveis segundo Porfírio
Gênero: "Aquilo que se predica relativamente a questão: ’O que é?’".
É uma unidade que reúne o conjunto das espécies, é aquilo ao qual a espécie se subordina. Também pode ser a origem de um sujeito, bem como uma característica predicada em relação a um indivíduo em comum. Por exemplo: O gênero dos Platônicos. Se retirado de um sujeito, suprimi-lo-à. O gênero é um predicado essencial.
Espécie: "É aquilo que está sob um gênero definido."
As espécies no gênero diferem por uma diferença específica, enquanto que internamente, diferem apenas por número. A espécie é um predicado essencial.
Diferença: "Aquilo mediante o qual a espécie excede o gênero em intenção".
No gênero animal, a diferença específica "capaz de raciocinar" da espécie humana excede o gênero em intenção, muito embora o gênero tenha essa diferença remotamente, ou em potência. A diferença se predica de várias espécies, não é exclusiva a uma. Caso a diferença seja retirada de um sujeito, suprimi-lo-à (no caso das diferenças específicas). A diferença é o fator que distingue as espécies - a diferença específica -. A diferença não é um predicado da essência. A diferença não apresenta gradação. A diferença específica enuncia a essência. A diferença simples não enuncia a essência.
Propriedade: "Aquilo que, sem expressar a essência de uma coisa, pertence, todavia, somente a ela e é convertível com ela".
Ou então "Pertence só a uma espécie, sempre a toda essa espécie". Caso a propriedade seja retirada de um sujeito, suprimi-lo-à. A propriedade é um predicado da essência, mas não faz parte dela. Contrariamente, deriva da essência. A propriedade não apresenta gradação.
Acidente: "Aquilo que pode pertencer ou não à mesma coisa".
Se um acidente separável for retirado de um sujeito, não suprimi-lo-à. Se um acidente inseparável for retirado de um sujeito, suprimi-lo-à. O acidente apresenta gradação.
Não há um consenso em se a série mnemônica foi composta por Guilherme de Sherwood ou Pedro Hispano. Essa série foi composta para que os alunos de lógica se lembrassem dos modos válidos do silogismo (representado pelos nomes) e também a forma pela qual cada silogismo deveria ser reduzido à primeira figura14. A redução é um processo pelo qual um silogismo em uma das figuras imperfeitas (II, III ou IV) é expresso como um silogismo de primeira figura, que é chamada de figura perfeita. As séries mnemônicas a seguir são um artifício que enumera os dezenove modos válidos das quatro figuras, indicando os métodos para reduzir os modos das figuras imperfeitas aos modos correspondentes da figura perfeita.
Série mnemônica:
Primeira figura: Barbara, Celarent, Darii, Ferio.
Segunda figura: Camestres, Cesare, Festino, Baroco.
Terceira figura: Darapti, Felapton, Disamis, Datisi, Bocardo, Ferison.
Quarta figura: Bamalip, Calemes, Dimatis, Fesapo, Fresison.
Aqui, convém dizer que a notação para as figuras que foi usada no curso não é a única; existe uma outra forma de classificar as figuras, que é segundo o número I, II, III, IV. Vamos introduzir essa notação só para fins de praticidade deste estudo, mas saiba que a forma proposta pelo Professor supera essa em simplicidade. Sempre que formos assistir aulas, convém sempre nos atermos a notação proposta pelo Professor, sem querer reinventar a roda. O propósito pelo qual estamos inserindo uma nova notação neste estudo é para que o aluno conheça outras formas de representar as mesmas coisas, até como exercício mental. As figuras sob esta perspectiva são:
Figuras:
Figura I: O termo médio é predicado da premissa menor e sujeito da premissa maior.
Figura II: O termo médio é predicado de ambas as premissas.
Figura III: O termo médio é sujeito de ambas as premissas.
Figura IV: O termo médio é predicado da premissa maior e sujeito da premissa menor.
Agora apresentaremos como decodificar a primeira série mnemônica apresentada: A chave para as séries mnemônicas é que as vogais indicam o modo nesta ordem tradicional: premissa maior, premissa menor, conclusão. Desta forma, “Barbara” corresponderia ao modo AAA, e as vogais dos demais nomes significam os modos do silogismo. É conveniente interpretar as series mnemônicas como sob a forma: premissa maior; premissa menor; conclusão.
B, C, D, F indicam a que modo correspondente da primeira figura serão reduzidos os modos das outras figuras. No modo Cesare, da segunda figura, a letra "s" indica que a proposição sob o modo E deve ser convertida simplesmente e com isso, o silogismo sob forma Cesare será convertido para a forma Celarent, através dos processos indicados.
Toda consoante com significado estará indicando o que a premissa mais próxima deverá sofrer para que o silogismo seja reduzido ao de primeira figura.
As consoantes também têm significados:
p (per accidens) significa que a proposição indicada pela vogal precedente precisa ser convertida por limitação. Uma proposição de modo A (Total afirmativa), por exemplo, seria convertida para uma proposição de modo I (Parcial afirmativa) e vice-versa.
s (simpliciter) significa que a proposição indicada pela vogal precedente será convertida simplesmente, colocando o sujeito na posição do predicado e o predicado na posição do sujeito.
m (muta) significa que as premissas devem ser transpostas.
c (per contradictorian propositionem) significa que a redução será indireta, por refutação de uma conclusão contraditória num silogismo de primeira figura.
r, b, l, n, t, d não têm significação.
Na forma Disamis, por exemplo, a premissa menor A deve ser convertida simplesmente, a conclusão I deve ser convertida simplesmente e as premissas devem ser transpostas, como indicado pela letra m. Desse modo, um silogismo sob a forma Disamis é reduzido à primeira figura sob a forma Darii.
Ou "imagem",↩︎
Para tratar de Deus, sempre tratamos em termos equívocos.↩︎
Vide. Árvore de Porfírio↩︎
Pois conhecimento só é conhecimento daquilo que nos é cognoscível.↩︎
Pois algo só é grande ou pequeno em relação a outras coisas.↩︎
O nome "Sócrates" que tem suplência discreta, não o seu predicado.↩︎
Pois exclui o sujeito de toda ela.↩︎
A depender do contexto, a distribuição pode variar.↩︎
Pois lembre-se, affirmo,↩︎
Pois lembre-se, nego.↩︎
Não se atenha tanto assim às palavras que são utilizadas, perceba que "certo" é só uma flexão de "certeza", mas nesse silogismo-exemplo, essas palavras são usadas para comunicar o mesmo conceito. Por isso, não se apegue às palavras, e sim aos conceitos que elas transmitem.↩︎
A saber, gênero, espécie, diferença específica, propriedade e acidente.↩︎
Lembre-se, [gênero mais próximo] + [diferença específica].↩︎
Os escolásticos (e até o próprio Aristóteles) diziam que a figura mais perfeita é a figura I, pois ela é a única capaz de sacar conclusões totais, que são mais fortes que parciais ou singulares.↩︎
Para ter acesso ao PDF do opúsculo, clique aqui.